OrbitHv logo OrbitHv

2019

프로그래밍언어 최종 과제

한국어 / English

진행 기간: 2019.04~06
작성: 2021-10-08 22:48:19 +0900
마지막 수정: 2021-10-11 22:47:09 +0900

Compiler Programming Language Python

제시된 문법으로 작성된 코드를 Assembly-like 코드로 변환합니다.

개요

이 문서는 2019년 1학기 프로그래밍언어 과목의 최종 과제의 내용을 정리한 문서이다. Github에 이 과제를 위한 Repository가 있고 관련 내용도 README.md에 정리되어있지만 내용을 복습하고 코드에 대한 설명도 간단히 첨부할 겸 새로 작성한다.

이 과제에서 요구하는 바는 아래와 같다.

과제 내용

여기에서 원문을 볼 수 있다. 아래는 이 파일의 내용을 정리한 것이다.

관련 이론

Scanner

Scanner의 기능은 입력받은 문자열을 Parser가 인식할 수 있는 단위인 토큰 단위로 구분하는 것이다. 이 토큰의 형식은 보통 정규 표현식1으로 정해지며, 주어진 입력이 만족하는 정규 표현식이 존재하지 않는 경우 작동을 중지하고 에러를 출력할 수 있다. 또한 Scanner는 추가적으로 Symbol Table의 기초적인 부분을 구성한다. 토큰을 만드는 과정에서 등장한 keyword나 수가 아닌 단어는 이 프로그램에 등장한다고 체크를 해놓는다.

Scanner의 구현은 Finite Automata를 사용한다. 그 중에서도 구상은 NFA가 더 쉽기 때문에 NFA의 형태로 구상한다. 하지만 이를 직접 구현하는 것은 난이도가 있는 것인지 구상한 NFA를 DFA로 변환한 후 이 DFA를 구현한다.2

DFA

DFA는 Deterministic Finite Automaton의 약자이다. DFA는 (Q,Σ,δ,q0,F)와 같은 집합으로 나타낼 수 있다.

이제 길이가 n인 어떤 문자열 w∈Σ*가 있다고 하자. 이 때의 작동 방식은 w를 구성하는 문자 순서대로 상태를 전이시킨다. 그리고 w의 문자를 모두 입력받은 후의 상태가 F에 포함되는지 확인하고 결과값을 출력한다. 이를 의사코드로 써보면 아래와 같다.

q[0] = q_0
for i in range(0, n):
    q[i+1] = δ(q[i], w[i])
print(q[n] in F)
NFA

NFA는 Non-deterministic Finite Automaton의 약자이다. NFA는 (Q,Σ,Δ,q0,F)와 같은 집합으로 나타낼 수 있다.

위의 DFA와 다른 점은 전이 함수의 함수값의 형태가 다르다는 것이다. DFA에서는 상태와 문자를 입력값으로 하여 상태 하나를 반환하는 전이 함수 δ였지만 NFA에서는 상태의 집합을 반환한다. 이를 고려하여 동작 메커니즘을 생각해보면 아래와 같다.

q[0] = set(q_0)
for i in range(0, n):
    q[i+1] = set()
    for x in q[i]:
        q[i+1] = union(q[i+1], Δ(x, w[i]))
print(!(q[n].intersect(F).empty()))
과제에 맞는 작동 방식 구상

FA의 전이 함수는 완전 함수일 필요가 없다. 이를 사용하여 토큰의 조건을 만족하는 경우에 대해서만 전이 함수의 함수값을 정의하고 이외의 경우에 대해서는 정의하지 않아 에러를 유발하는 방식을 사용할 것이다. 에러가 발생하면 지금까지 입력받은 문자를 기반으로 토큰을 생성한 후, 처음 위치로 돌아가 해당 문자(공백 문자는 그 다음 문자)를 다시 전이 함수에 대입하여 과정을 반복하는 방법을 사용하면 된다.

여기에 Symbol Table도 여기서 일부 구성한다. 대입(=) operator가 나오면 바로 앞의 토큰을 확인하여 토큰의 값을 Symbol Table에 등장하는 변수의 이름으로 추가한다.4

Parser

Parser는 기본적으로 Scanner로부터 생성된 토큰을 입력받아 코드가 문법에 맞는지 체크하는 기능을 한다. 문법은 보통 과제에서 주어지는 것처럼 Production rule의 형태로 주어진다.

보통 Parser는 PDA(Pushdown Automaton)으로 구현하는데, 이 경우 Production rule을 그대로 사용할 수는 없기 때문에 주어진 문법을 오토마타의 종류에 맞는 transition table로 변환한다. 비교적 간단한 문법의 경우 SLR(1)이나 LR(0)을 사용한다. LR Parser는 Shift와 Reduce라는 동작을 통해 Stack을 조작하여 문자열이 문법에 맞는지 판단한다. 어떤 상황에서 어떤 동작을 사용할지는 LR Parser의 파생형인 SLR, CLR, LALR마다 조금씩 다르다. 과제에서 주어진 문법의 경우 간단한 편이기 때문에 SLR(1)로 구현이 가능하므로 SLR(1)에서의 transition table을 구성하는 방법에 대해 서술한다.

Transition Table의 구성(SLR(1))

간단한 문법이 아래와 같이 주어져있다고 가정하자.

E → E "+" T
E → T
T → T "*" F
T → F
F → n

이 문법은 Context-free grammar에 속하며, G=(V,Σ,R,S) 형식으로 정의할 수 있다. 그 의미와 위 문법에서의 예시는 아래와 같다.

위에서 언급한 E' → E $ 문법을 추가한 후 • 기호를 도입한다. 이 기호는 오토마타가 현재 어느 지점을 읽고 있는지를 의미한다. 이 기호를 도입하기 전에 Production rule에 존재하는 ε-transition을 없애고 시작해야 한다. 이 예시의 경우는 ε-transition이 없기 때문에 처리할 것은 없지만 과제의 문법은 처리할 문법이 몇 가지 존재한다.

우선 starting state로 정의한 E’에 대하여 적용한다.

E' → •E $
E → •E "+" T
E → •T
T → •T "*" F
T → •F
F → •n

위와 같이 • 기호 바로 뒤에 있는 것이 non-terminal 기호인 경우는 해당 non-terminal을 좌항으로 가지고 있는 문법에 대해서 재귀적으로 적용한다. 이제 위 블럭 전체를 하나의 상태로 정의한다. q0라고 하겠다. 이 상태에서 E, T, F, n을 각각 하나 읽은 상태를 의미하는 상태를 만들어보겠다.

위의 4개의 상태 중 첫 2개의 상태는 terminal인 +와 *를 읽은 이후의 상태를 또 만들 수 있을 것이다.

각 상태를 만들어보니 • 기호가 non-terminal 앞에 가게 되면서 여러 production rule이 상태에 다시 추가되었다. 이러한 방법을 계속 사용하여 가능한 모든 상태를 만들면 transition table 생성에 사용할 다이어그램이 완성된다. 여기서 주의할 점은 상태 전이 시 FA와 다르게 non-terminal도 정의역에 포함된다. 즉, 정의역이 (V∪Σ)이다. 이를 바탕으로 그림을 그려보면 아래와 같이 될 것이다.

Diagram for example

이제 transition table에 사용하기 위해 각 non-terminal(이 문법의 경우는 E, T, F까지 총 3개이다)에 대하여 FOLLOW 집합을 만든다. FOLLOW 집합은 이 non-terminal 바로 다음에 올 수 있는 terminal 문자의 집합이다. 5

Non-terminal FOLLOW
E’ {$}
E {+}∪FOLLOW(E’)={$, +}
T {*}∪FOLLOW(E)={$, +, *}
F FOLLOW(T)={$, +, *}

이를 사용하여 transition table을 만드는 것은 아래와 같은 방법으로 진행한다.

  1. Table을 하나 만들고, 세로줄에는 상태의 번호, 가로줄에는 terminal과 $(EOF)을 모두 넣고 starting symbol을 제외한 non-terminal을 그 옆에 넣는다. terminal의 항 위에는 Action, non-terminal의 항 위에는 Goto라고 이름을 붙인다.
  2. 다이어그램에서 각 상태마다 terminal에 의한 transition은 S(도착 상태 번호)(shift), non-terminal에 의한 transition은 (도착 상태 번호)의 형식으로 추가한다. EOF가 허용된 상태에서 EOF를 입력받는 경우는 Acc 또는 A라고 표시한다.
  3. 어떤 상태에서 하나 이상의 문법에 대하여 • 기호가 오른쪽 끝에 가있는 경우 reduce 작업이 필요하다. production rule 형태에서 해당 문법의 번호를 가져와서 R(번호)의 형태로 transition table에 추가한다. 이 때 문법의 좌변에 해당하는 non-terminal의 FOLLOW 집합에 속해있는 terminal의 위치에만 추가한다.

이러한 작업을 거치면 아래와 같이 transition table을 생성할 수 있다.

(0) E' → E $
(1) E → E "+" T
(2) E → T
(3) T → T "*" F
(4) T → F
(5) F → n
ActionGoto
n+*$ETF
0S6187
1S2Acc
2S637
3R1S4R1
4S65
5R3R3R3
6R5R5R5
7R4R4R4
8R2S4R2
Transition Table을 활용한 Parser 구현

위에서 쓰던 예시를 그대로 사용하겠다. Parser를 구현할 때에는 스택(Parsing Stack)과 임시 변수(Lookahead)가 하나 필요하다. 문자열을 처리하면서 어떤 상태로 파싱을 진행하는지 저장하는 용도이다. 이 변수를 사용하면 PDA는 아래와 같이 작동한다. 예시로 n*n+n을 파싱해보겠다.

Input Parsing Stack Lookahead Operation
n*n+n$ 0 n S6
*n+n$ 0 n 6 * R5(F→n)
*n+n$ 0 F 7 * R4(T→F)
*n+n$ 0 T 8 * S4
n+n$ 0 T 8 * 4 n S6
+n$ 0 T 8 * 4 n 6 + R5(F→n)
+n$ 0 T 8 * 4 F 5 + R3(T→T*F)
+n$ 0 T 8 + R2(E→T)
+n$ 0 E 1 + S2
n$ 0 E 1 + 2 n S6
$ 0 E 1 + 2 n 6 $ R5(F→n)
$ 0 E 1 + 2 F 7 $ R4(T→F)
$ 0 E 1 + 2 T 3 $ R1(E→E+T)
$ 0 E 1 $ Acc

위 과정을 통해 예시의 문자열은 문법을 만족하는 문자열임을 알 수 있다. 그리고 연산의 종류에 따른 PDA의 작동 방식은 아래와 같이 될 것이다.

개발

과제 조건에서 부득이한 경우 문법을 변경할 수 있고, 그 내용과 이유를 보고서에 기입하도록 되어있다. 그래서 실제 개발에 대한 내용을 작성하기 전에 문법에 관련된 내용부터 작성한다.

문법 변경

주어진 문법을 읽고 이해하는 과정에서 몇 가지 이상한 점을 발견했다. 그 내용은 아래와 같다.

  1. block이 ε이 될 수 있다. block이 직접적으로 포함되어있는 prog 입장에서는 word "(" ")"에서 함수를 선언하고 그 뒤로 함수의 내용이 있어야 하는데 block이 ε이면 함수의 내용이 없는 것이다. 즉, 선언만 하고 구현하지 않는 경우이다. 이 문법에 따르면 함수 선언은 프로그램에서 단 한 번 등장하고 함수 호출은 없기 때문에 함수를 구현하지 않고 선언만 하는 것은 의미가 없다. 따라서 block이 ε이 되는 경우를 문법에서 배제했다.
  2. word와 num이 ε이 될 수 있다. ε이 된 경우 expr를 살펴보겠다. expr ::= expr "+" fact의 부분에서 fact가 ε이 될 수 있으므로 3+++4+와 같은 식도 올바른 코드가 된다. 또한 stat에서도 stat ::= word "=" expr ";"인 문법이 있는데, 여기서 word가 ε라고 하면 =7;도 올바른 코드이다. 하지만 위 두 경우 모두 일반적인 프로그래밍 언어에서는 잘못된 코드이며 Pseudocode Instruction로 구현하는 데에 있어서도 어려움이 있을 것이다. 따라서 word와 num의 와일드카드 *를 +로 대체했다.

위 내용을 적용한 문법은 아래와 같다.

prog    ::=   word "(" ")" block ;
block   ::=   "{" slist "}" ;
slist   ::=   slist stat
        |     stat ;
stat    ::=   IF "(" cond ")" THEN block ELSE block
        |     WHILE "(" cond ")" block
        |     word "=" expr ";"
        |     ;
cond    ::=   expr ">" expr
        |     expr "<" expr ;
expr    ::=   fact
        |     expr "+" fact ;
fact    ::=   num
        |     word ;
word    ::=   ([a-z] | [A-Z])+ ;
num     ::=   [0-9]+

Scanner

코드에서 등장할 수 있는 문자([a-zA-Z0-9\+\>\<\=\(\)\{\}\;]\s)에 대하여 token이 될 수 있는 경우를 구분한다. 우선 +, >, <, =은 operator, {, }, (, ), ;은 separator, IF, THEN, ELSE, WHILE은 keyword로 분류한다. 그리고 [0-9]+은 num, keyword를 제외한 [a-zA-Z]+은 word로 분류한다. 분류한 내용을 바탕으로 다이어그램을 그린다.

NFA

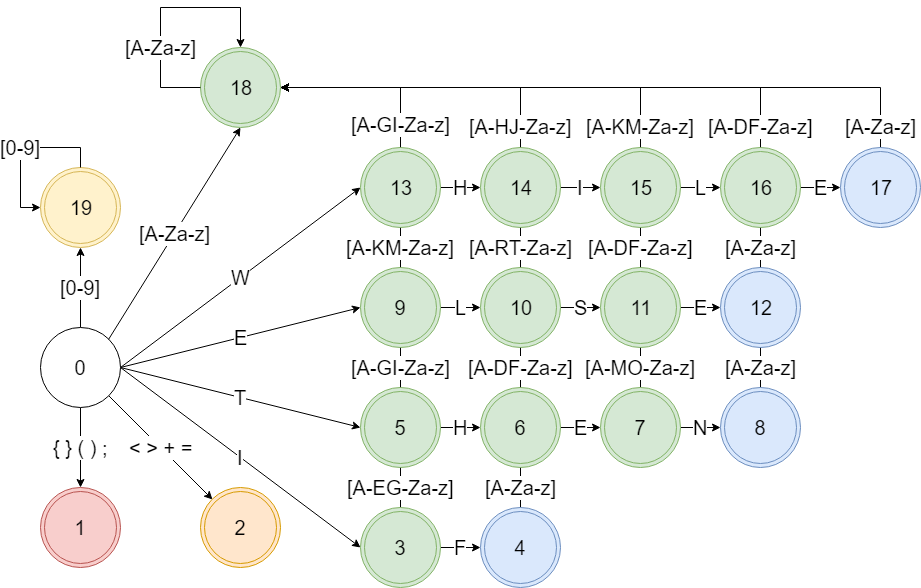
원래는 NFA를 DFA로 고치고 이를 모두 구현해야했으나… Python을 사용하여 비교적 편하게 개발했다. Python은 set과 같은 자료구조를 따로 import하지 않아도 사용할 수 있고 사용법도 단순하여 쉽게 사용했다. 거기에 문자열 관련해서도 다른 언어에 비해 비교적 적은 코드를 사용하여 구현할 수 있기 때문에 Python을 사용하여 개발하기로 했다.

위에서 분류한 문자(열)에 따라 그 종류를 구분한다. 종류별로 해당되는 문자(열)를 변수에 저장하고 한 글자씩 읽으면서 토큰을 구성한다. 이 중에서 keyword는 문자가 아닌 특정한 문자열이므로 한 번에 여러 글자를 체크하여 keyword인지 체크해야 하고, num과 word는 같은 종류의 문자가 여러 번 나오므로 한 번 문자가 나왔을 때 그 뒤로 같은 종류인 위치까지 계속 읽어야 한다. 토큰을 구성하는 도중에 공백 문자가 나온다면 탐색을 중지하고 현재까지 읽은 문자열로 토큰을 만들어야 한다.6 여기에 Scanner의 기능 중 하나인 프로그램에 나타날 symbol을 저장하는 역할도 구현해야 한다. symbol은 word 토큰에서만 나올 수 있으므로 word 토큰을 읽을 때마다 이를 저장한다. 이를 고려해서 의사코드를 짜보면 아래와 같이 된다.

separators = ['(', ')', '{', '}', ';']
operators = ['+', '<', '>', '=']
keywords = ["IF", "THEN", "ELSE", "WHILE"]
digits = ['0', '1', '2', ... , '9']
letters = ['A', 'B', 'C', ... , 'Z', 'a', 'b', ... ,'z']
whitespaces = [' ', '\n', '\r', '\t']
tokens = []
symbols = set()

while not input.eof():
    l = 0
    if input[0] in separators:
        tokens.append(("separator", input[0]))
        input.next(1)
    else if input[0] in operators:
        tokens.append(("operator", input[0]))
        input.next(1)
    else if input[0] in whitespaces:
        input.next(1)
    else if (l = is_keyword(input)):
        tokens.append(("keyword", input[0:l]))
        input.next(l)
    else if (l = is_num(input)):
        tokens.append(("num", input[0:l]))
        input.next(l)
    else if (l = is_word(input)):
        tokens.append(("word", input[0:l]))
        symbols.append(input[0:l])
        input.next(l)

fun is_keyword(input): // keyword인 경우 해당하는 keyword의 길이를 반환
    for keyword in keywords:
        l = keyword.length()
        if input[0:l] == keyword:
            return l
    return 0

fun is_num(input): // num인 경우 길이를 반환
    l = 0
    while input[l] in digits:
        l++
    return l

fun is_word(input): // word인 경우 길이를 반환
    l = 0
    while input[l] in letters:
        l++
    return l

과제 당시에는 조금 급하게 만든 감이 없지 않아 있어서 불필요한 코드나 비효율적인 알고리즘이 일부 들어가있다. 소스 코드는 여기에서 볼 수 있다.(과제는 시간에 상관없이 돌아가기만 하면 됐다.)

Parser

문법 조정

Parser에서는 토큰을 기반으로 문법이 맞는지 체크하기 때문에 토큰의 종류에 맞게 Parser용 문법을 만들어야 한다. 예를 들어, 과제의 문법에서 num ::= [0-9]+와 같은 규칙은 토큰과 전혀 상관없는 규칙이기 때문에 빼준다. 여기에 우변이 ε인 규칙은 처리하기 힘드므로 다른 규칙에 ε인 경우를 적용하여 제거해준다. 그러면 과제의 문법이 아래와 같이 조정된다.

prog    ::= word "(" ")" block ;
block   ::= "{" slist "}"
        |   "{" "}" ;
slist   ::= slist stat
        |   stat ;
stat    ::= IF "(" cond ")" THEN block ELSE block
        |   WHILE "(" cond ")" block
        |   word "=" expr ';' ;
cond    ::= expr ">" expr
        |   expr "<" expr ;
expr    ::= fact
        |   expr "+" fact ;
fact    ::= num
        |   word ;

이제 이 문법을 기반으로 다이어그램을 그려야 하는데, 위 문법을 그대로 쓰면 매우 복잡해지므로 약자를 사용한다. non-terminal은 대문자로, terminal은 소문자로 쓴다는 규칙을 적용하여 아래 표와 같이 변환시킨다.

수정 전 수정 후 수정 전 수정 후
prog P IF i
block B THEN t
slist L ELSE e
stat S WHILE h
cond C word w
expr E num n
fact F    

이를 사용하여 문법을 production rule의 형식에 맞게 다시 적어보면 아래와 같다.

(0)     P   ->  w "(" ")" B
(1)     B   ->  "{" L "}"
(2)     B   ->  "{" "}"
(3)     L   ->  L S
(4)     L   ->  S
(5)     S   ->  i "(" C ")" t B e B
(6)     S   ->  h "(" C ")" B
(7)     S   ->  w "=" E ";"
(8)     C   ->  E ">" E
(9)     C   ->  E "<" E
(10)    E   ->  F
(11)    E   ->  E "+" F
(12)    F   ->  n
(13)    F   ->  w
SLR parser 다이어그램

위에서 조정한 문법을 사용해서 SLR parser 다이어그램을 그려보면 아래와 같다.

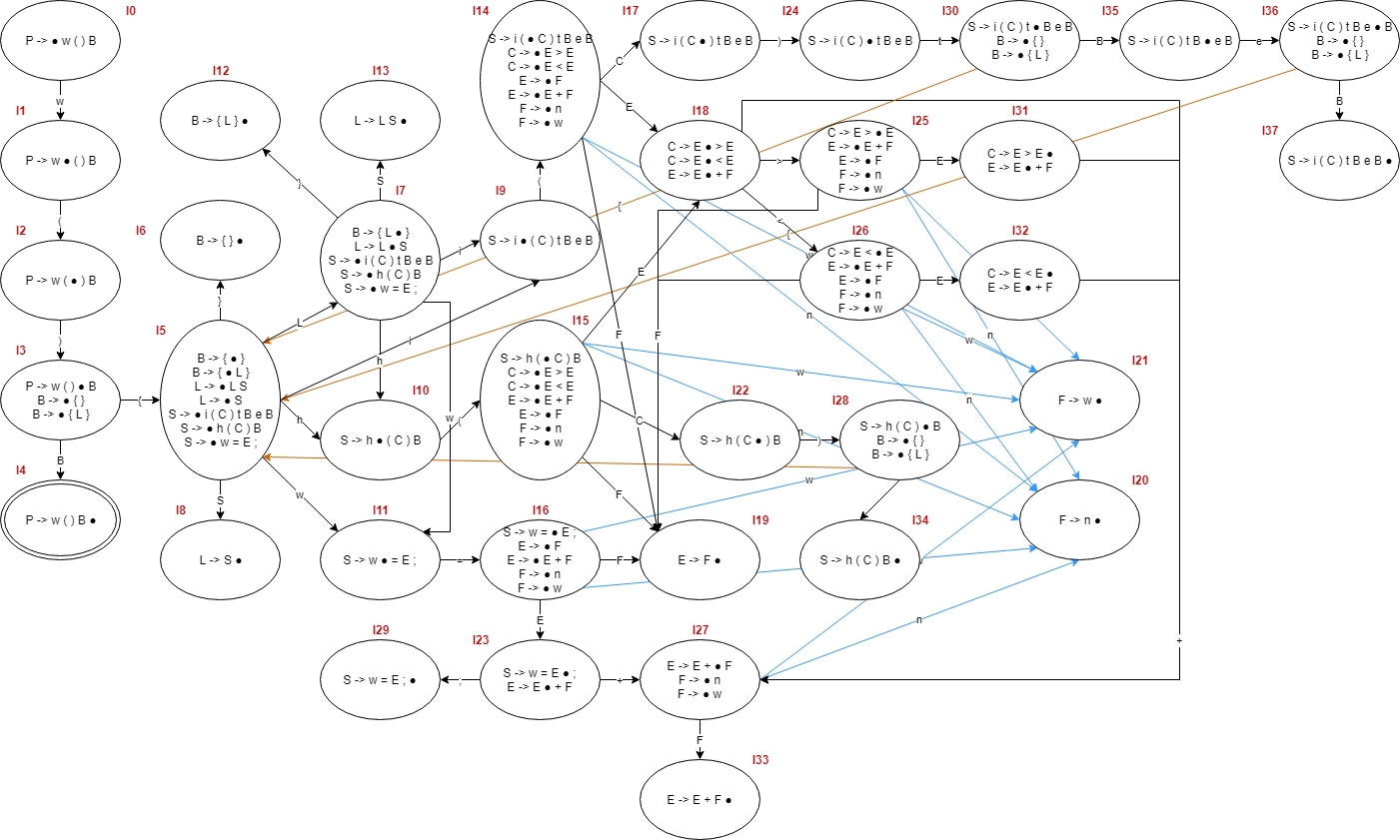
Diagram for SLR Parser

FIRST & FOLLOW 집합

위의 문법을 기반으로 non-terminal의 FIRST와 FOLLOW 집합을 만들면 아래와 같이 된다.

FIRST(P) = { w }
FIRST(B) = { '{' }
FIRST(L) = FIRST(S) = { i, h, w }
FIRST(S) = { i, h, w }
FIRST(C) = FIRST(E) = { n, w }
FIRST(E) = FIRST(F) = { n, w }
FIRST(F) = { n, w }

FOLLOW(P) = { $ }
FOLLOW(B) = { e } ∪ FOLLOW(P) ∪ FOLLOW(S) = { e, $, '}', i, h, w }
FOLLOW(L) = { '}' } ∪ FIRST(S) = { '}', i, h, w }
FOLLOW(S) = FOLLOW(L) = { '}', i, h, w }
FOLLOW(C) = { ')' }
FOLLOW(E) = { ';', '>', '<', '+'} ∪ FOLLOW(C) = { ';', '>', '<', '+', ')' }
FOLLOW(F) = FOLLOW(E) = { ';', '>', '<', '+', ')' }
Parsing Table

위에서 구한 SLR Parser의 다이어그램과 FOLLOW 집합을 사용하여 parsing table을 구해보면 아래와 같이 된다.

다이어그램 펼치기/숨기기
StateActionGoto
nwiteh><=+;(){}$BLSCEF
0S1
1S2
2S3
3S54
4Acc
5S11S9S10S678
6R2R2R2R2R2R2
7S11S9S10S1213
8R4R4R4R4
9S14
10S15
11S16
12R1R1R1R1R1R1
13R3R3R3R3
14S20S21171819
15S20S21221819
16S20S212319
17S24
18S26S25S27
19R10R10R10R10R10
20R12R12R12R12R12
21R13R13R13R13R13
22S28
23S27S29
24S30
25S20S213119
26S20S213219
27S20S2133
28S534
29R7R7R7R7
30S535
31S27R8
32S27R9
33R11R11R11R11R11
34R6R6R6R6
35S36
36S537
37R5R5R5R5

구현

Scanner는 Python을 사용하여 다소 쉽게 구현했지만 Parser는 정직하게 구현한다. 먼저 위에서 구성한 Parsing Table을 그대로 옮긴다. 각 state별로 dict를 하나씩 할당하여 Action과 Goto 상관없이 입력받은 non-terminal와 terminal에 따른 행동을 저장한다. 예를 들어, 0번 state의 변수는 {'w': 'S1'}이 된다. 이를 사용하여 PDA의 작동 방식 그대로 파싱을 구현한다. 여기에 추가적으로 Symbol Table의 각 symbol마다 scope도 정해주어야 한다. 이 작업은 Parsing Tree를 구성한 후 tree의 depth를 사용하여 구하면 편하므로 파싱 과정에서 parsing tree를 만들도록 한다. 이 과정을 의사 코드로 작성하면 아래와 같이 된다.

table = [{'w': ['S', 1]}, {'(', ['S', 2]}, ...]
grammar = [['P', "w()B"], ['B', "{L}"], ['B', "{}"], ...]
state = 0
stack = [0]
nodes = []

while i < tokens.length():
    action = table[state][tokens[i].type]
    if action == None:
        throw error("Parsing Error: Unexpected token(" + tokens[i] + ")")
    if action[0] == 'A': // Accept
        break
    else if action[0] == 'S': // Stack
        state = action[1]
        stack.push(tokens[i])
        stack.push(state)
        // Parsing tree
        node = {"value": tokens[i].value}
        nodes.append(node)
    else if action[0] == 'R': // Reduce
        gram = grammar[action[1]]
        action = table[state][gram[0]]
        for i in range(0, 2 * gram[1].length()):
            stack.pop()
        stack.push(gram[0])
        stack.push(action[1])
        // Parsing tree
        node = {"value": tokens[i].value, "children": nodes[-gram[1].length():0]}
        nodes = nodes[0:nodes.length() - gram[1].length()]
        nodes.append(node)
root = {}
root.value = grammar[0][0]
root.children = nodes

위 코드에서 사용된 tokens 변수는 토큰의 종류와 실제 값을 dict 형식으로 저장한 변수의 배열이다. 종류와 실제 값이 둘 다 필요한 이유는 num 토큰이나 word 토큰이 parsing 과정(문법 체크 과정)에서는 종류, symbol table 구성 과정에서는 토큰의 실제 값을 사용하기 때문이다. 나머지 토큰은 type과 value가 같다.

위 코드의 동작이 끝나면 root 변수에 parsing tree가 생긴다. 이를 사용하여 각 symbol의 유효 scope를 찾는다. 중괄호 토큰이 나오면 그에 맞게 scope를 조정하고, symbol을 정의하는 구문(w=E;)이 나오면 symbol table의 symbol 항목에 scope를 저장한다. 그 과정은 아래의 의사 코드와 같다.

stack = [root]
level = -1
scope = []
current = {}
prev = {}

while not stack.empty():
    prev = current
    current = stack.pop()
    if current.value == '{':
        level += 1
        if scope.length() < level + 1:
            scope.append(0)
        scope[level] += 1
        for i in range(level + 1, scope.length()):
            scope[i] = 1
    else if current.value == '}':
        level -= 1
    else if current.value == '=':
        symbol_table.set_scope(prev.value, scope[0:level+1].join("."))
    
    if current.children != null:
        for i in range(current.length() - 1, -1, -1):
            stack.push(current.children[i])

실제 코드에서는 위와 같은 방법을 그대로 사용하지는 않았다. tokens로 넘어오는 정보의 종류도 약간 다르고, 그에 따라 처리하는 방법도 약간 다르며 scope를 처리하는 부분도 약간 다르다. 실제로 사용한 코드는 여기에서 볼 수 있다.

Code Generator

Parser에서 생성된 parsing tree를 사용하여 어셈블리와 닮은 목표 언어로 변환한다. 과제에서 목표 언어와 관련되어 제시된 내용은 아래와 같다.

우선 목표 언어 변환할 statement를 설정해놓은 다음 parsing tree를 순회하면서 해당 statement를 목표 언어로 변환하는 방법을 사용할 수 있다. 예를 들어 h(C)B 구문이 나오면 JUMPF instruction을 활용할 수 있다. 그리고 해당 구문 안의 C나 B 같은 부분은 해당 부분을 따로 목표 언어로 만든 뒤 기존 코드에 붙이면 된다. 간단하게 설명하면 아래와 같다.

.L1:
(C에 해당하는 코드, 결과를 Reg#1에 저장)
JUMPF Reg#1, .L2
(B에 해당하는 코드)
JUMP .L1
.L2:

이러한 식으로 목표 언어로 변환할 수 있다. 이를 구문 별로 어떻게 할지 정해놓고 parsing tree를 순회하면서 목표 언어를 만들면 된다. symbol의 경우 symbol table에 해당 symbol을 저장할 주소를 넣어놓고 사용하면 된다. 이를 의사 코드로 표현하면 아래와 같다.

current = {}
reg = 1
label = 1
addr = 0
max_reg = 0

fun gen_code(node):
    code = ""
    if node.type == 'P': // P -> w()B
        code = "BEGIN " + node.children[0].value + "\n"
        code += gen_code(node.children[3]) // B
        code += "END " + node.children[0].value + "\n"
        return code
    if node.type == 'B':
        if node.children.length() == 2: // B -> { }
            return ""
        return gen_code(node.children[1]) // B -> { L }
    else if node.type == 'L':
        code = gen_code(node.children[0]) // L or S
        if node.children.length() == 2: // L -> L S
            code += gen_code(node.children[1])
        return code
    else if node.type == 'S':
        if node.children[0].type == 'i': // S -> i ( C ) t B e B
            code += gen_code(node.children[2]) // C
            code += "JUMPF Reg#" + reg + " .L" + label + "\n"
            code += gen_code(node.children[5]) // B1
            code += "JUMP .L" + (label + 1) + "\n"
            code += ".L" + label + "\n"
            code += gen_code(node.children[7]) // B2
            code += ".L" + (label + 1) + "\n"
            label += 2
        else if node.children[0].type == 'h': // S -> h ( C ) B
            code += ".L" + label + "\n"
            code += gen_code(node.children[2]) // C
            code += "JUMPF Reg#" + reg + " .L" + (label + 1) + "\n"
            code += gen_code(node.children[4]) // B
            code += "JUMP .L" + label + "\n"
            code += ".L" + (label + 1) + "\n"
            label += 2
        else: // S -> w = E ;
            code = gen_code(node.children[2]) // E
            code += "ST Reg#" + reg + " " + addr + "\n"
            table.set_addr(node.children[0].value, addr)
            addr += 4
        max_reg = max(max_reg, reg)
        return code
    else if node.type == 'C':
        code = gen_code(node.children[0]) // E1
        reg += 1
        code += gen_code(node.children[2]) // E2
        reg -= 1
        if node.children[1].value == '<': // C -> E < E
            code += "LT Reg#" + reg + " Reg#" + reg + " Reg#" + (reg + 1) + "\n"
        else: // C -> E > E
            code += "LT Reg#" + reg + " Reg#" + (reg + 1) + " Reg#" + reg + "\n"
        max_reg = max(max_reg, reg + 1)
        return code
    else if node.type == 'E':
        if node.children[0].type == 'E': // E -> E + F
            code = gen_code(node.children[0]) // E
            reg += 1
            code = gen_code(node.children[2]) // F
            reg -= 1
            code += "ADD Reg#" + reg + " Reg#" + reg + " Reg#" + (reg + 1) + "\n"
            max_reg = max(max_reg, reg + 1)
            return code
        else: // E -> F
            return gen_code(node.children[0]) // F
    else if node.type == 'F':
        if node.children[0].type == 'w': // F -> w
            code = "LD Reg#" + reg + " " + table.get_addr(node.children[0].value) + "\n"
        else: // F -> n
            code = "LD Reg#" + reg + " " + node.children[0].value + "\n"    
        max_reg = max(max_reg, reg)
        return code

print(gen_code(root))

위와 같은 방식을 사용하여 목표 언어와 사용한 레지스터의 개수를 출력할 수 있다. 레지스터의 개수를 최소화하는 방법은 모든 변수를 ST와 LD를 사용하여 필요할 때마다 꺼내쓰는 것이다. 변수를 저장하는 구문은 w=E;밖에 없기 때문에 여기서 무조건 ST를 실행시키면 레지스터를 아무리 사용하더라도 값을 안전하게 저장할 수 있다. 여기에 시작 언어가 변수를 새로 선언하는 구문이 없는 언어이므로 scope를 신경쓰지 않고 해당 이름을 가지는 변수가 유일하게 존재한다고 가정해도 된다.

과제로 이를 구현할 때는 돌아가기만 하면 됐기 때문에 조금 오류가 있을 수도 있다. 당시 작성한 파일은 여기에서 볼 수 있다.

Result

내용 추가 예정

  1. Regular Expression, 줄여서 Regex라고 한다. 기본적인 regex(문자(열)와 Concatenation, Alternation, Kleene Star의 3가지 연산의 조합으로 이루어진 regex)는 유한 상태 오토마타로 변환이 가능하고 역과정도 가능하다. ↩

  2. set 자료구조를 사용하여 NFA를 구현할 수 있다.↗ DFA에서 현재 상태를 하나의 변수로 저장하는 것을 NFA에서 현재 가진 상태를 set에 저장하는 방법이다. 전이함수를 나타내는 변수만 NFA에 맞게 새로 정의하면 나머지는 DFA와 크게 차이가 없을 것 같다. ↩

  3. 전이 함수의 정의만 따져보면 정의역이 Q×Σ이기 때문에 여기에 속하는 모든 원소에 대해서 함수값을 정의해야 할 것처럼 보이지만 꼭 그렇지는 않다. DFA에서 나올 수 있는 조합에 대해서만 함수값이 정의되어도 DFA는 오류 없이 잘 작동한다. ↩

  4. 대입 연산자가 아니더라도 스캔 과정에서 등장하는 모든 word는 Symbol Table에 넣으면 된다. Parser가 동작하면서 scope가 정의되지 않는 symbol이 있거나 선언에 의해 정해진 symbol의 scope 밖에서 symbol이 등장하면 에러를 출력하면 된다. 이 글을 작성하는 과정에서 헷갈려서 위키피디아를 찾아보니 대입 연산자 앞에 있는 토큰만 처리한다는 조건은 적혀있지 않았다. ↩

  5. 경우에 따라서 FIRST 집합도 사용한다. FIRST 집합은 non-terminal을 구성하는 첫 번째 terminal로서 올 수 있는 terminal의 집합이다. SLR parsing 과정 자체에서는 FIRST를 사용하지 않지만, FOLLOW 집합을 구할 때 유용하게 사용할 수 있다. 문법의 규칙 중 우변에서 non-terminal이 연달아 나오는 경우에 FIRST 집합이 쓸모있다. 예를 들어 E → T F라는 규칙이 있을 때, FOLLOW(T)는 항상 FIRST(F)를 부분집합으로 가진다. 예시로 제시한 문법은 이러한 경우가 없었지만 과제의 문법은 이러한 경우가 있으므로 여기서는 서술하지 않지만 과제 결과물 구상에서는 이를 사용할 것이다. ↩

  6. 조금 더 구체적으로 설명하자면, abc de라는 문자열을 처리해야 한다고 하자. a를 읽은 시점에서 word 토큰을 구성하기 시작한다. b와 c를 읽은 후 공백 문자를 입력받게 되는데, 이 때에는 abc에서 끊고 이를 하나의 word 토큰으로 인식해야 한다. 공백 문자 이후의 문자열인 de를 읽고나면 위 문자열은 abcde라는 word 토큰이 아닌 abc와 de의 2개의 word 토큰으로 인식해야 하는 것이다. ↩