진행 기간: 2021.06~07
마지막 수정: 2022-12-04 15:08:53 +0900

Godot Rhythm Game

중심의 정다각형과 그 정다각형으로 다가가는 노트...

• 목차

계기

군대에서 신병 휴가를 즐긴 후 2주 간 분리를 하게 되었는데¹, 당시 24시간 아무것도 안하면서도 핸드폰은 17:30~21:00에만 사용할 수 있어서 매우 심심했다. 같이 생활하던 병사들은 너무 할 게 없어서 공부를 하거나 독서를 하는 등 일반적인 군생활을 하면서 절대 안 할 것 같은 일을 하곤 했다. 나는 딱히 책도 없고 해서 다른 학교 컴퓨터공학과인 동기의 전공책(운영체제)을 빌려서 조금씩 읽었는데, 그마저도 몇 페이지 읽지 못하고 때려쳤다. 차라리 그 동기와 게임 아이디어나 하나 만들어보는 것이 나을 것 같아서 각자 아이디어를 생각하고 토론하는 방식으로 시간을 때웠다. 나는 최근 가장 많이 플레이하던 장르인 리듬게임에 대해 생각해봤는데, 아무리 생각해봐도 단순 낙하형이나 중심에서 바깥으로 멀어지는 방식은 너무 진부했다. 이미 다 있는 것들이었다². 그래서 중심에 특정 모양이 있고 노트가 그 중심 도형 위로 모여드는 방식은 어떨까해서 이 컨셉으로 몇 가지 경우를 구상해보기로 했다.

구상

기본 컨셉

아이디어 #1

• 중심이 정n각형이고 n은 게임이 진행되는 동안 가변
• 노트의 길이가 중심의 정n각형의 변의 길이과 같음

아이디어 #2

• 중심이 정n각형이고 n은 게임이 진행되는 동안 가변
• 노트가 정n각형을 확대한 후 한 변만 따온 모양

아이디어 #3

• 중심이 원이고 노트의 모양이 원호

선택

우선 아이디어 #3은 아무리 봐도 Lanota를 뒤집은 것으로 밖에 보이지 않아 일찍이 배제되었다. 아이디어 #1은 같이 아이디어를 고민하던 동기가 노트는 화면 전체에서 떨어지는데 터치는 화면 전체를 사용하지 않아 비효율적인 것 같다고 하여 아이디어 #2로 결정했다. 슈퍼 헥사곤하고 좀 많이 닮은 것 같다

아이디어 #2를 선택한 후 중심 도형을 삼각형으로 하는 플레이 화면을 간단히 그려봤는데, 그리고 나니 마치 프리즘을 옆면에서 바라보는 느낌이 났다. 그래서 이 프로젝트의 이름이 Project Prism이 되었고, 전반적인 컨셉을 이쪽으로 잡기로 했다.

점수 체계

점수 체계에도 세부적으로 결정해야 하는 것이 있기에 세부 항목으로 분리하였다. 개발 당시 정리하던 파일은 여기에서 볼 수 있다.

만점

구상 초기에는 플레이하던 게임에서 사용하는 만점 시스템에 대해 알아본 후 비교해본 후 결정하기로 했다. 우선 1,000,000, 100.00%, 노트 점수 고정 방식이 있음을 생각했고 개발할 때 다시 정하기로 했다.

개발하면서 정리한 내용은 아래와 같다.

• 1,000,000
  • 사용하는 게임: Cytus, VOEZ, Lanota, Dynamix, OverRapid 등 다수
• 100.00%
  • 사용하는 게임: Deemo, ADOFAI, Cytus(TP) 등
  • Deemo는 데이터 파일을 분석해본 결과 실제로는 1,000,000 만점의 정수형으로 저장하는 것으로 판별
  • ADOFAI는 100.00%+(매우 정확)×0.01%, 즉, 가능한 최대 점수가 100.00%이 아니고 100.00+(노트 수)×0.01%이다.
• 10,000,000
  • 사용하는 게임: Arcaea
  • Arcaea는 더욱 정확한 판정에 대해 노트 당 1점씩 더 부여한다. 다만 만점을 굳이 10,000,000으로 설정한 것은 기타 판정(Good, Miss)보다 가중치를 훨씬 작게 설정하여 Good과 Miss를 더 많이 냈지만 이 판정으로 인하여 순위가 역전되는 상황을 만들지 않게 하기 위함으로 추측한다.³
• 노트 수에 비례한 점수
  • 일반적으로 이 경우 콤보에 대한 점수는 할당되어있지 않다.
  • 이 경우 채보마다 만점이 달라서 플레이어의 순위를 매기는 경우 단순평균이 아닌 다른 방법을 사용해야 한다.

콤보

초기 격리 중에 아이디어를 구상할 때에는 $n\log{n}$ 방식으로 정했다. 수식으로 표현하자면 노트 n개의 채보에서 최대 콤보 m을 만들면 $\frac{m\log{m}}{n\log{n}}$에 비례한 콤보 점수를 받아가는 것이다.

개발 중에는 뭔가 특이한 콤보 공식($n\log{n}$도 특이하긴 하지만 더 특이한 것이 필요했다)을 넣고 싶었다. Geogebra를 사용해서 이것저것 실험해보았는데, 그 때 찍어놓은 스크린샷은 아래와 같다. 왜 이런거 하냐고 물어보신다면 할 말이 없습니다

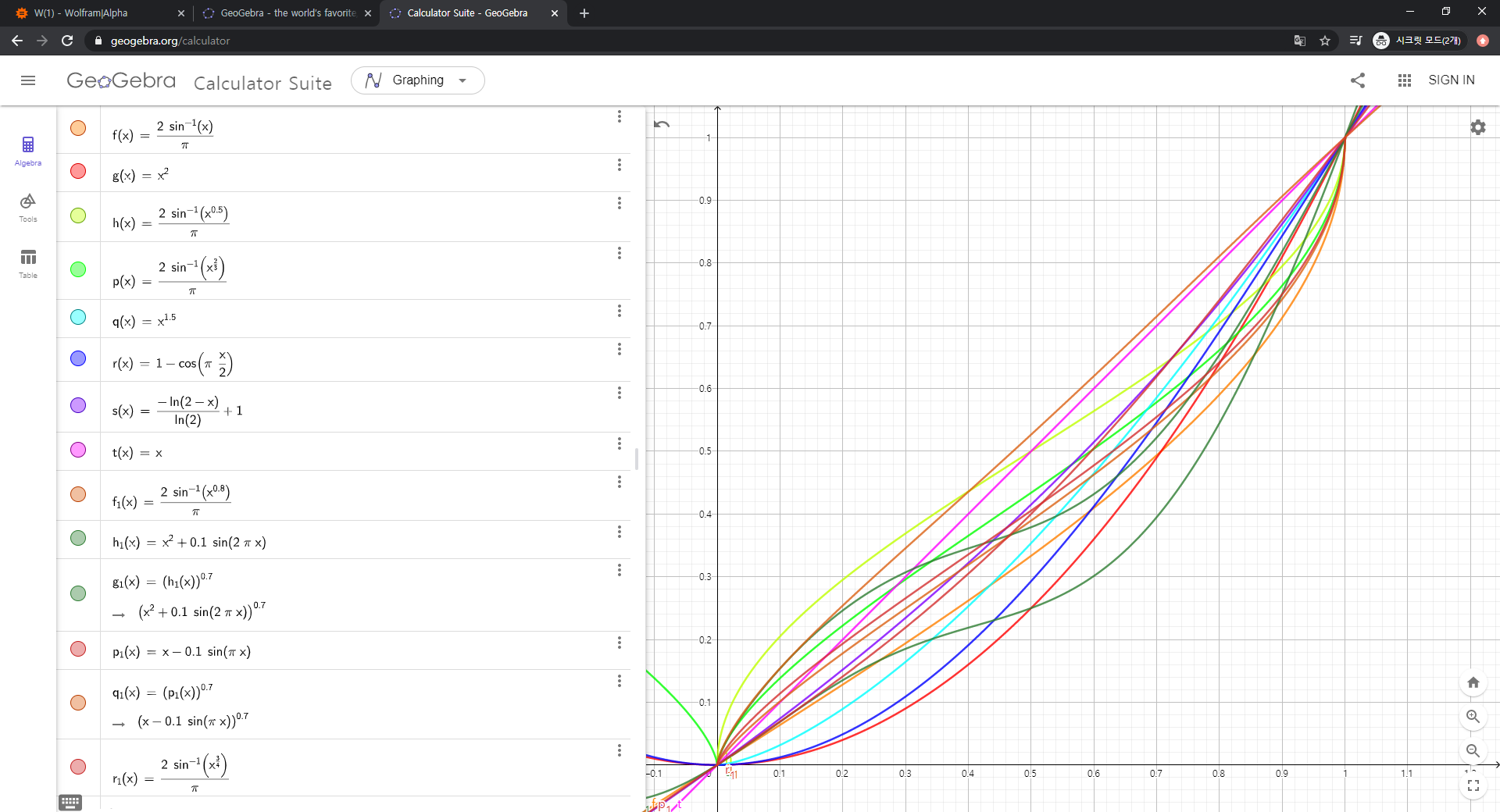
그 중 나의 의도에 맞는 콤보 공식을 오랜 시도 끝에 얻었다. 그 식은 아래와 같다.

\[\frac{m}{n}-0.1\frac{\sin{((\frac{m}{n})^{1.5}\pi)}}{\sin{({0.5}^{1.5}\pi)}}\]

이 식을 x, x²와 비교한 그림과 풀콤보 대비 얻을 수 있는 점수는 아래와 같다.

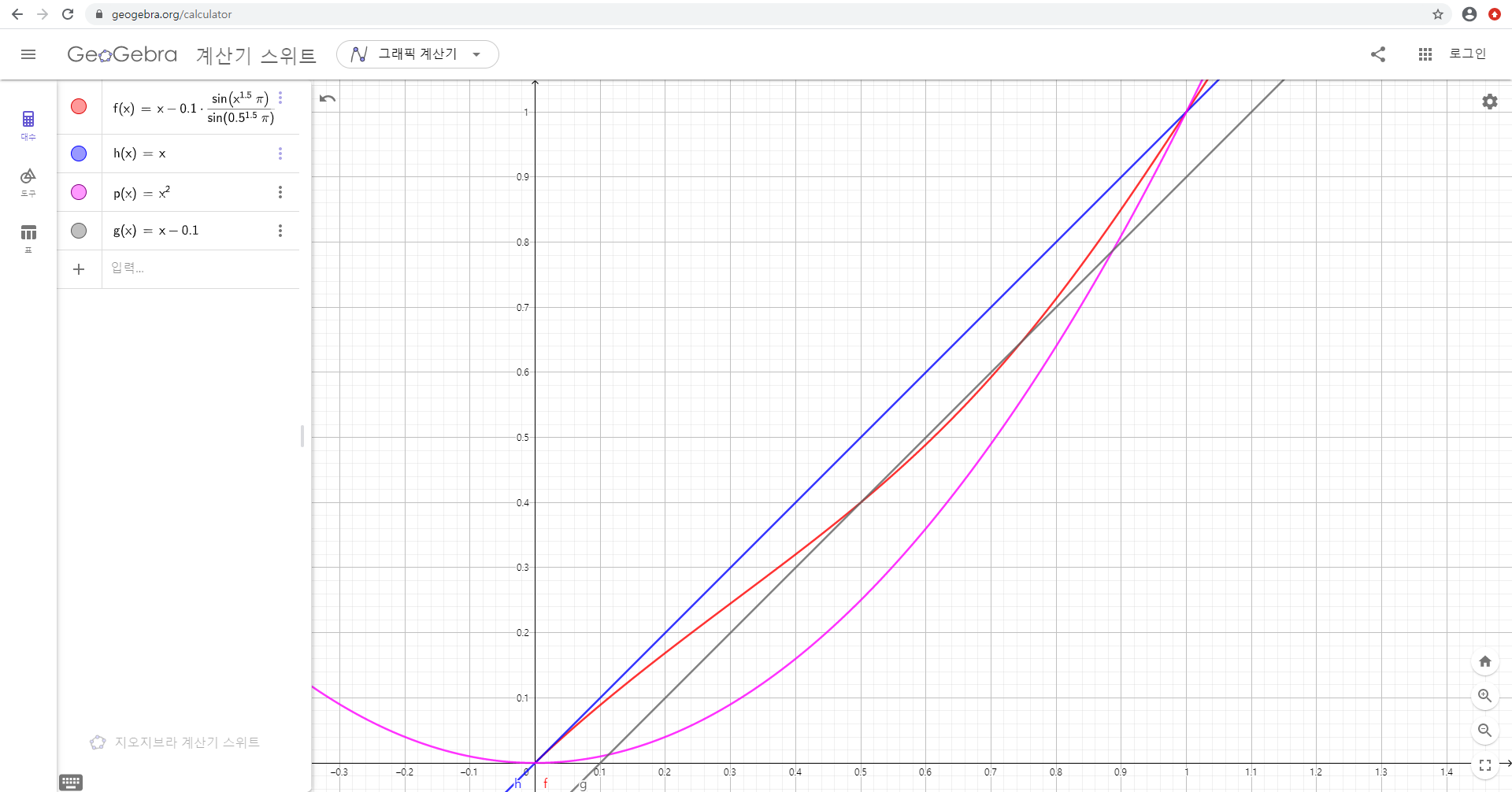
콤보 대비 점수 비율

콤보	점수
0%	0%
5%	4.6081%
10%	8.8931%
15%	12.9749%
20%	16.9051%
25%	20.7291%
30%	24.4913%
35%	28.2413%
40%	32.0348%
45%	35.9326%
50%	40%
55%	44.3035%
60%	48.9079%
65%	53.8714%
70%	59.2412%
75%	65.0483%
80%	71.3019%
85%	77.9854%
90%	85.0528%
95%	92.4269%
100%	100%

대략적으로 0% 근처에서는 풀콤보 대비 콤보 비율과 점수 비율이 비슷했고, 중후반 구간에서는 10%정도 차이가 남을 알 수 있다.⁴ 위 그림에서 회색 선이 콤보 비율과 점수 비율이 10% 차이나는 지점을 찾기 위해 그은 보조선이다.

인게임 애니메이션

초기(격리 중)

우선 총 6가지의 애니메이션을 구현하는 것으로 했다. 그 목록은 아래와 같다.

명칭	변수	설명
Translation	pos[Vector2]	카메라 이동 혹은 중심 도형 이동
Rotation	deg[float]	중심 도형 회전
Zoom	magnifier[float]	카메라 수직 이동 혹은 중심 도형 확대/축소
Add_Side	dst_side[int]	중심 도형 변 개수 증가
Remove_Side	dst_side[int]	중심 도형 변 개수 감소
Center_Rotation	deg[float]	카메라 회전

노트

터치 노트

채보 파일

기타

---

1. 당시 코로나바이러스감염증-19에 대한 방침은 휴가 복귀일을 지정하여 휴가를 나간 병사들이 일괄적으로 복귀할 수 있도록 하는 것이었고, 휴가 복귀 시 일반 병사와 분리된 공간에서 휴가 복귀한 병사들과 같이 2주간 생활을 하는 것이었다. ↩

2. 단순 낙하형은 생각해봐도 아주 많았다. 단순 낙하형하면 Deemo나 탭소닉, OverRapid 등 가장 흔한 타입이었다. 여기에 머리를 조금 써서 두 축방향으로 낙하하는 costheta(서로 알지는 못하지만 학교 선배가 팀 총괄로 제작한 리듬게임이다), 판정선 기준 양쪽에서 떨어지는 STATIC이나 판정선이 세 방향으로 놓여있는 Dynamix, 가로선이 자유롭게 움직이는 VOEZ, 판정선이 낙하하는 Cytus와 DJMax Technika 등 바리에이션도 웬만한 것은 다 있었다. 거기에 중심에서 바깥으로 멀어지는 방식은 아케이드 게임은 Maimai, 모바일 게임은 Lanota, Stellights, Hachi Hachi 등 이미 다 있었다. ↩

3. 극단적인 예시를 들어보자면, 모든 노트를 Perfect로 처리했으나 모두 일반 Perfect인 경우의 점수가 하나를 제외한 모든 노트를 Super Perfect(공식 명칭 아님)으로 처리하고 나머지 하나는 Good으로 처리한 경우의 점수보다 높아야 한다. 즉, Good 판정으로 인해 잃은 점수가 매우 정확 판정으로만 얻을 수 있는 점수보다 커야 한다는 의미이다. ↩

4. 애초에 여러 함수를 테스트해보면서 초반에는 $y=x$와 비슷하고 후반은 $y=x^{1.5}$와 비슷한 함수를 찾고 있었다. 거기에 50% 콤보 구간에서 점수가 정확히 40%가 나오는 것이 좋겠다 생각했다. 이 조건을 꽤 잘 만족하는 위 함수에 정확히 풀콤보의 반을 대입하면 함수값이 0.4가 나온다. ↩